Problem Overview

In LeetCode 172: Factorial Trailing Zeroes, we are asked to find the number of trailing zeros in a factorial of a given number n. This problem is a classic example of mathematical algorithms and number theory in competitive programming.

Directly calculating n! to count zeros is inefficient for large numbers, so the challenge is to find a clever, optimized approach to determine the trailing zeros without computing the factorial itself.

For example, if the input is n = 100:

  • The factorial 100! ends with 24 trailing zeros.
  • This occurs because the number of factors of 5 in the factorial determines the trailing zeros.

This problem is widely asked in C++ coding interviews and online programming contests. It helps to improve understanding of efficient counting algorithms and factorial properties.

Factorial Trailing Zeroes

Problem Difficulty & Tags

LeetCode 172: Factorial Trailing Zeroes as a Medium difficulty problem. It is commonly asked in C++ coding interviews and because it requires understanding of factorials and efficient counting techniques.

Topics / Tags:

  • Mathematical algorithms
  • Number theory
  • Factorial properties
  • Counting techniques
  • Optimization in C++

The main challenge in this problem is to count trailing zeros efficiently without calculating the entire factorial, which makes it a great example of algorithmic optimization in coding interviews and competitive programming.

Approach / Logic Explanation

When I first saw LeetCode 172: Factorial Trailing Zeroes, I knew calculating n! directly wouldn’t work for large numbers. So, I focused on the fact that trailing zeros come from factors of 10, which are made from 2 × 5 pairs. Since there are always more 2s than 5s in a factorial, counting the number of 5s is enough to find the zeros.

Here’s how I approached the problem step by step:

  1. Initialize a variable res = 0 to store the total count of trailing zeros.
  2. Use a loop to divide n by 5 repeatedly and add the quotient to res. Each division counts the multiples of 5, 25, 125, etc., which contribute extra zeros.
  3. Stop the loop when n / 5 becomes 0. At this point, all factors of 5 are counted.
  4. Return res as the total number of trailing zeros in n!.

I like this approach because it’s efficient, O(log n) time, and avoids huge factorial computations. It also helps me practice number theory and optimization techniques in coding interviews.

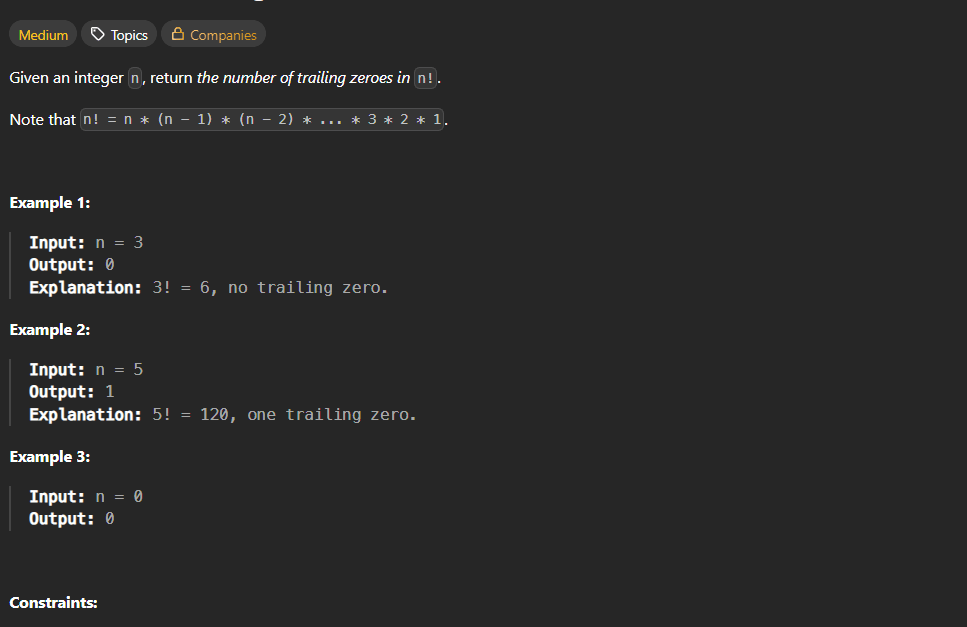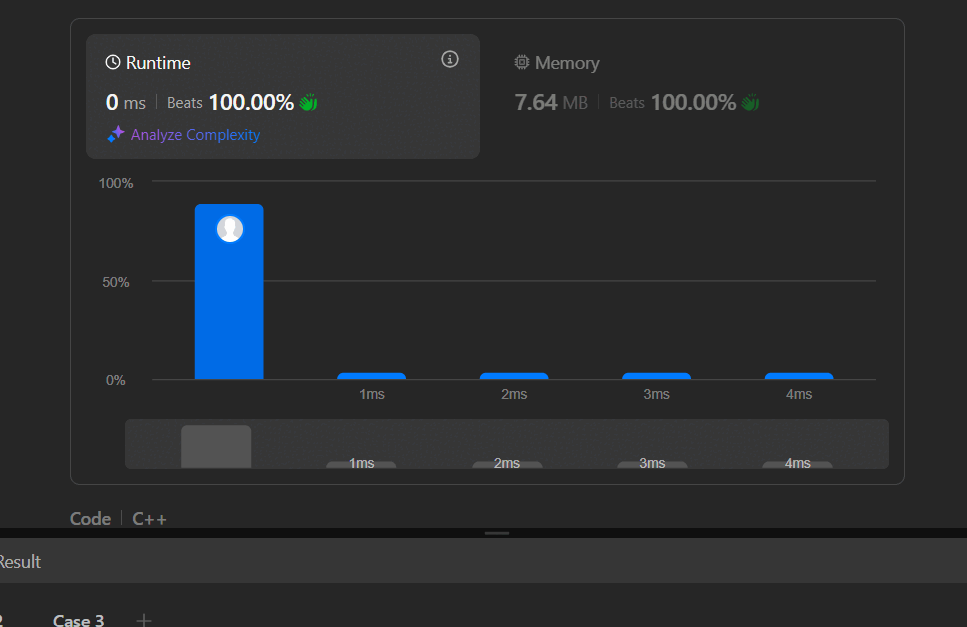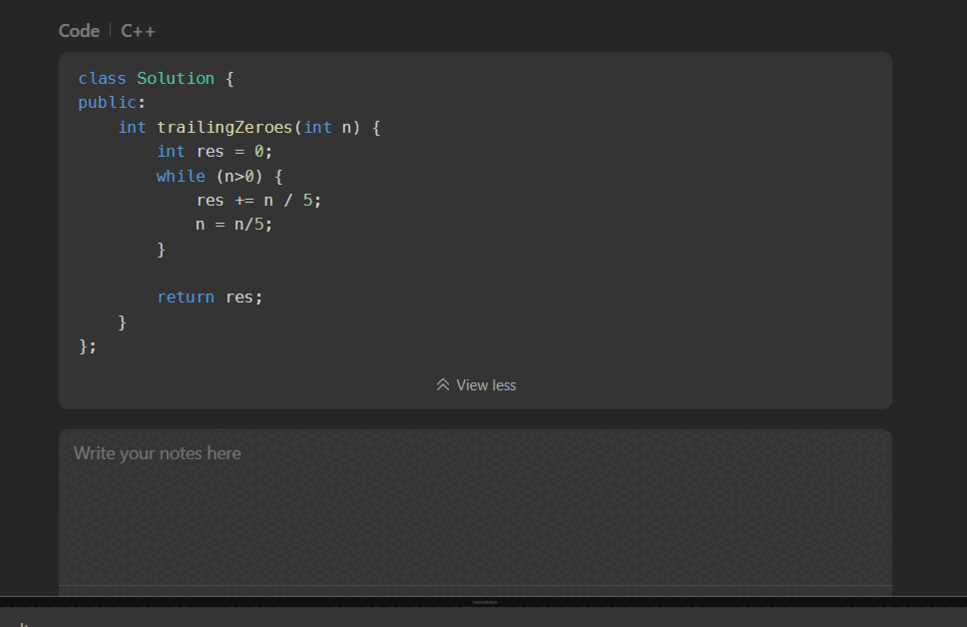
Solution Code

Based on the logic I explained, here’s the C++ solution I implemented for this problem:


class Solution {
public:
    int trailingZeroes(int n) {
        int res = 0;
        while (n > 0) {
            res += n / 5;
            n = n / 5;
        }
        return res;
    }
};

I wrote this code to efficiently count all factors of 5 in n!. Each iteration adds the multiples of 5, 25, 125, etc., directly to res. This avoids calculating the factorial itself, which would be impossible for large n.

Step-by-Step Walkthrough

Let me explain how my solution works using an example: n = 100.

  1. Initialization: I start with res = 0 to keep track of trailing zeros.
  2. Iterative Division: I divide n by 5 repeatedly:
    • First iteration: 100 ÷ 5 = 20 → add 20 to res.
    • Second iteration: 20 ÷ 5 = 4 → add 4 to res.
    • Third iteration: 4 ÷ 5 = 0 → stop the loop.
  3. Final Result: The total trailing zeros in 100! is res = 24.

This method is efficient because it avoids calculating large factorials and directly counts the factors of 5, which determine the trailing zeros.

Time & Space Complexity Analysis

After writing the solution, I analyzed how efficient it is:

Time Complexity

The loop divides n by 5 repeatedly until it becomes 0. The number of iterations is proportional to log5(n). So, the time complexity is O(log n).

Space Complexity

I only use a single variable res to store the count. No extra space depends on the input size, so the space complexity is O(1).

This makes the solution very efficient even for large numbers like n = 10^9.

Mistakes to Avoid & Tips

Warning: Don’t forget that factors of 25, 125, etc., contribute extra zeros. Only counting n/5 will give incorrect results for large n.
Common Error: Trying to calculate factorial directly will cause overflow even for moderate n. Always use the division method.
Pro Tip: Remember that the number of trailing zeros depends on the number of 5s, not 2s, because 2s are always more abundant in n!.
Note: This solution works efficiently even for very large n, making it ideal for coding interviews and competitive programming.

Sample Input & Output

To make it easier to understand, here’s how the function works with some example inputs:

Input Output Explanation
3 0 3! = 6 has no trailing zeros.
5 1 5! = 120 has 1 trailing zero.
100 24 Count multiples of 5, 25, 125…: 100/5=20, 100/25=4, 100/125=0 → total 24 zeros.

Related Problems

If you found this problem interesting, you might also like these similar challenges:

Conclusion

Solving LeetCode 172: Factorial Trailing Zeroes was a good exercise in understanding how factorials work and how to optimize computations. I realized that directly calculating n! is impractical for large numbers, and focusing on counting factors of 5 gives an efficient solution.

Key takeaways from this problem:

  • Trailing zeros in a factorial are determined by the number of 5s in its factors.
  • Dividing n by 5, 25, 125… efficiently counts the zeros without computing the factorial.
  • The solution works in O(log n) time and O(1) space, suitable for large input values.

I encourage you to try similar math-based problems to strengthen your understanding of number theory and algorithm optimization. These techniques are very useful for coding interviews and competitive programming.