HackerRank Roads and Libraries Problem Solution in C++ | DFS Approach Explained

Problem Overview

The HackerRank Roads and Libraries problem is a classic graph problem where we need to build libraries and/or repair roads in a city to ensure that every citizen has access to a library. The challenge is to minimize the total cost given the cost of building a library and the cost of repairing a road.

The input provides the number of cities (n), the number of roads (m), the cost of building a library (cl), the cost of repairing a road (cr), and the list of city connections (roads). The goal is to calculate the minimum cost to provide library access to all citizens.

The key observation is that if building a library is cheaper than repairing a road (cl < cr), it is optimal to build a library in every city. Otherwise, we can use DFS traversal to find connected components and decide where to build libraries and repair roads efficiently.

This problem is a great exercise in graph traversal, connected components, and cost optimization strategies.

Problem Difficulty & Tags

The Roads and Libraries problem on HackerRank is generally considered a Medium-level problem. It requires understanding of graph traversal techniques and cost optimization strategies.

• Difficulty: Medium
• Tags: Graphs, Trees, Depth First Search (DFS), Connected Components, Cost Optimization

This problem is a good practice for handling large-scale graphs and thinking carefully about how to minimize total costs while satisfying all constraints. It’s a popular example in coding interviews and competitive programming challenges.

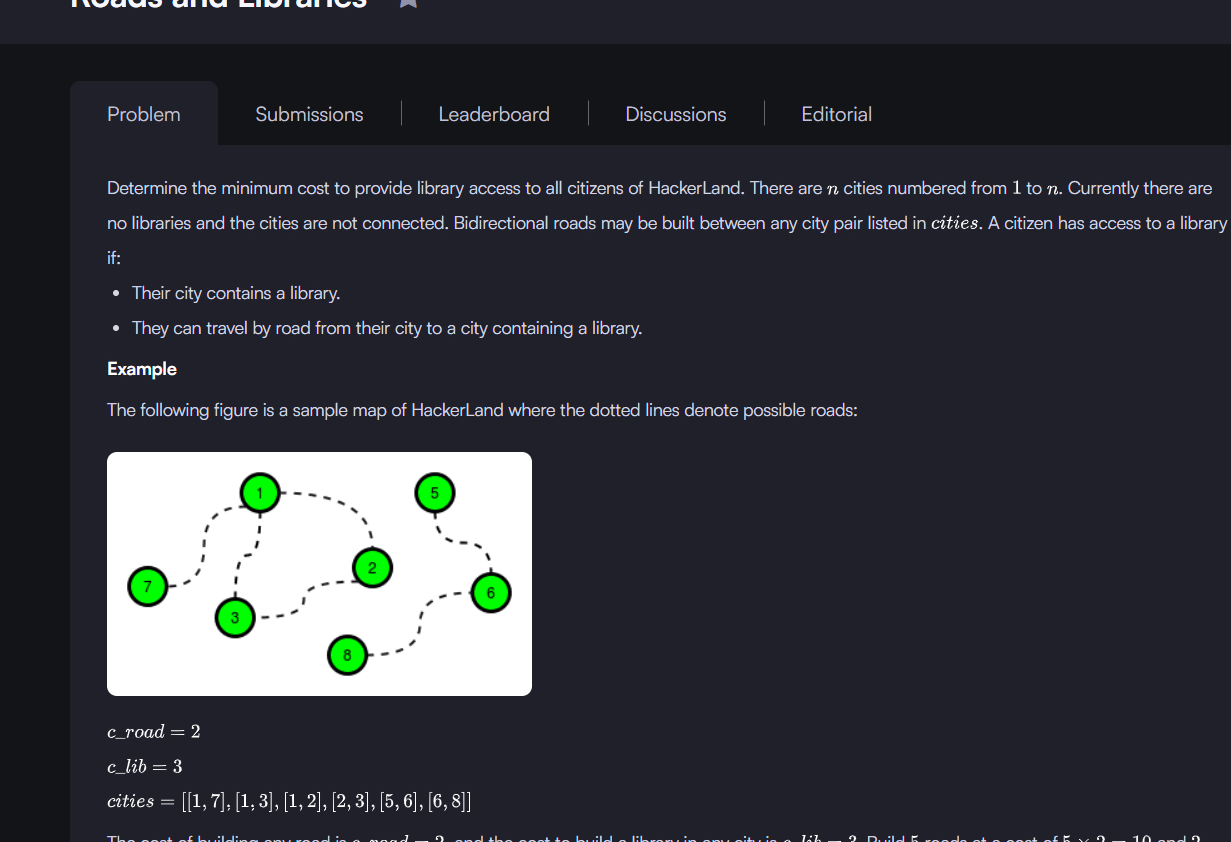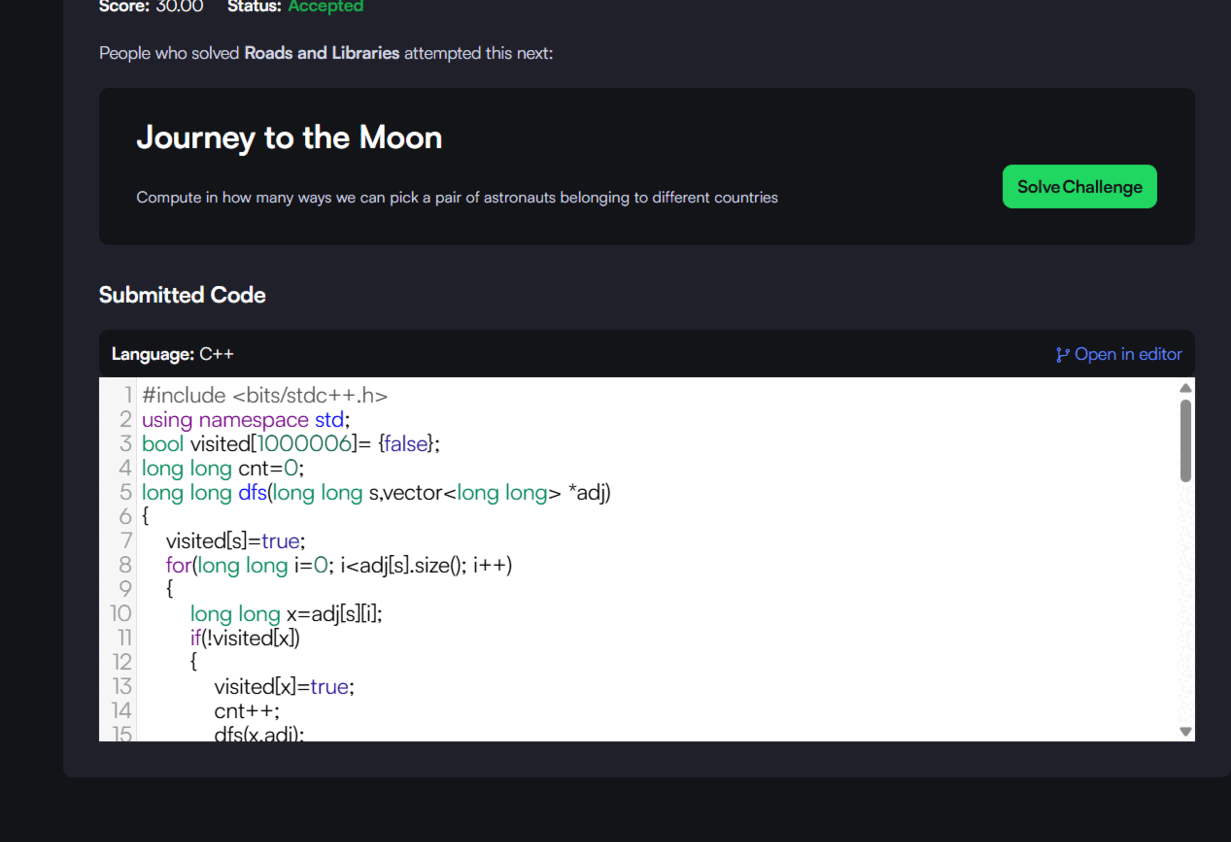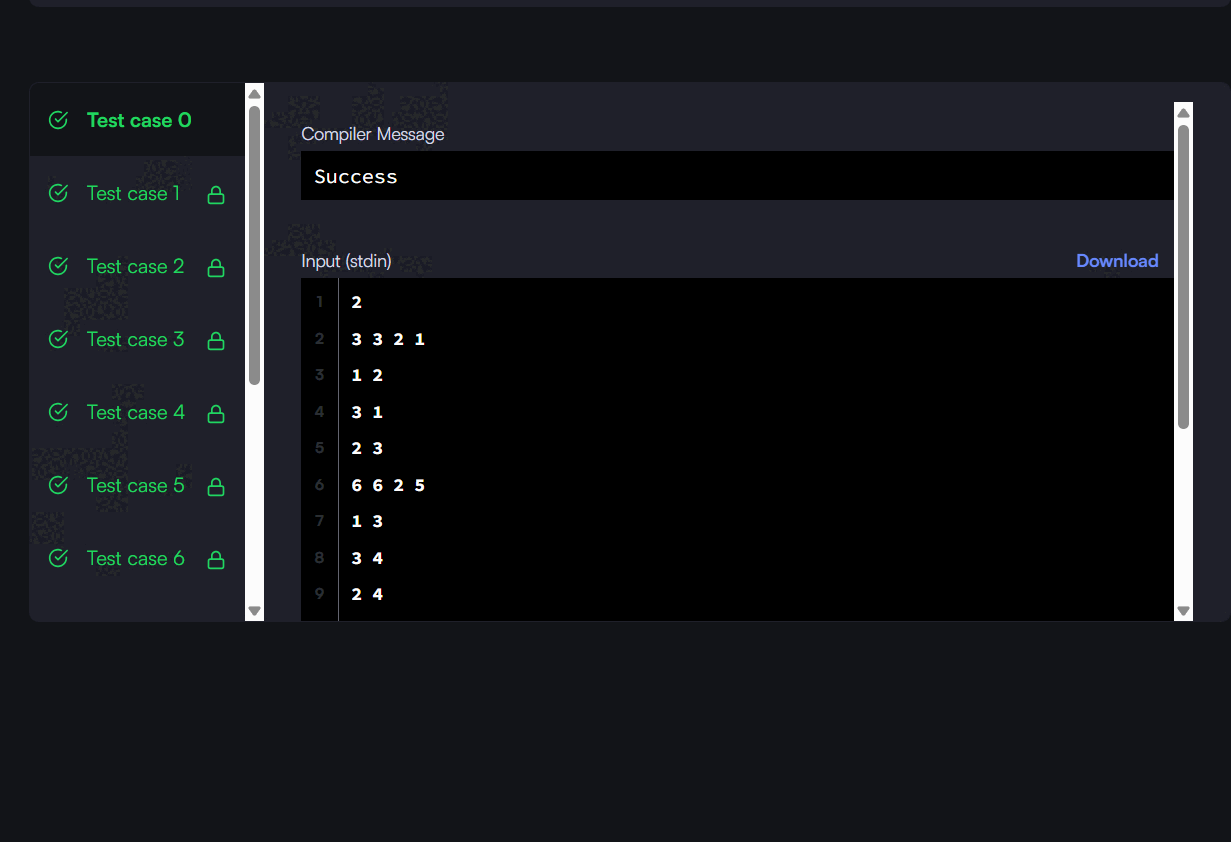
Understanding the Problem

The Roads and Libraries problem asks us to make sure every city has access to a library, either by building one in the city or by repairing roads to connect it to a city that already has a library. The challenge is to do this at the minimum total cost.

The input gives us the number of cities (n), the number of roads (m), the cost of building a library (cl), the cost of repairing a road (cr), and a list of city connections. The key task is to decide where to build libraries and which roads to repair to achieve the least cost.

One important observation is that if building a library is cheaper than repairing a road (cl < cr), it’s optimal to just build a library in every city. Otherwise, we need to use DFS traversal to identify connected components and calculate how many libraries and roads are needed for minimum cost.

Understanding this structure is crucial because it allows us to apply DFS efficiently, count components, and optimize our solution for both correctness and performance.

Approach / Logic Explanation

To solve the Roads and Libraries problem efficiently, I followed a simple DFS-based approach combined with cost analysis. Here’s the logic step by step:

1. First, check if building a library is cheaper than repairing a road (cl < cr). If so, it’s cheaper to build a library in every city. The total cost is simply n * cl.
2. If repairing roads is cheaper, we need to find connected components in the graph. I used DFS to traverse the graph starting from unvisited cities.
3. For each connected component, I count the number of roads that need to be repaired to connect all cities in that component. I also count one library per component since at least one library is needed.
4. The total cost is then calculated as total = (cl * number_of_libraries) + (cr * number_of_roads).
5. Repeat this process for each query if multiple test cases are provided.

Using DFS ensures that each city is visited exactly once per query, making the solution efficient even for large graphs. This approach handles both small and large connected components and guarantees the minimum cost.

Solution Code (C++ Implementation)

Below is my C++ implementation for the Roads and Libraries problem. It uses DFS to find connected components and calculate the minimum cost for libraries and roads.

#include <bits/stdc++.h>
using namespace std;

bool visited[1000006] = {false};
long long cnt = 0;

long long dfs(long long s, vector<long long> *adj) {
    visited[s] = true;
    for(long long i = 0; i < adj[s].size(); i++) {
        long long x = adj[s][i];
        if(!visited[x]) {
            visited[x] = true;
            cnt++;
            dfs(x, adj);
        }
    }
    return cnt;
}

int main() {
    long long n, m, q;
    cin >> q;
    while(q--) {
        long long cr, cl, i, j, u, v, cnt_road = 0, cnt_lib = 0, total;
        cin >> n >> m >> cl >> cr;

        memset(visited, 0, sizeof(visited));
        vector<long long> adj[1000006];

        for(i = 0; i < m; i++) {
            cin >> u >> v;
            adj[u].push_back(v);
            adj[v].push_back(u);
        }

        if(cr > cl) {
            cout << n * cl << endl;
        } else {
            for(i = 1; i <= n; i++) {
                if(!visited[i]) {
                    cnt = 0;
                    cnt_lib++;
                    cnt_road += dfs(i, adj);
                }
            }
            total = (cr * cnt_road) + (cl * cnt_lib);
            cout << total << endl;
        }
    }

    return 0;
}

Step-by-Step Walkthrough

Let’s break down how my DFS-based solution works with a more detailed example:

Example:

Number of cities (n) = 10
Number of roads (m) = 8
Cost of library (cl) = 3
Cost of road (cr) = 2
Roads:
1 - 2
1 - 3
2 - 4
2 - 5
3 - 6
6 - 7
8 - 9
9 - 10
    

1. Check Library vs Road Cost: Since cr < cl, repairing roads can reduce total cost, so we proceed with DFS.
2. DFS Traversal: Start DFS from unvisited cities. Starting from city 1, DFS visits 1 → 2 → 4, 5 → 3 → 6 → 7. All cities in this connected component are counted for roads and 1 library is added.
3. Second Component: DFS starts at city 8, visiting 8 → 9 → 10. This is another connected component, so we add 1 library and count the roads used.
4. Count Libraries and Roads: Component {1,2,3,4,5,6,7} adds 1 library and 6 roads. Component {8,9,10} adds 1 library and 2 roads.
5. Calculate Total Cost: Total cost = (cl * number_of_libraries) + (cr * number_of_roads) = (3*2) + (2*8) = 22.

This walkthrough demonstrates how DFS efficiently identifies connected components, counts the required libraries and roads, and calculates the minimum total cost for a larger, more complex graph.

Sample Input & Output

Here’s an example to illustrate how the input is processed and the corresponding output:

Time & Space Complexity Analysis

Time Complexity

The DFS traversal visits each city and each road exactly once. Since there are n cities and m roads, the overall time complexity is O(n + m). This ensures the solution runs efficiently even for large graphs with hundreds of thousands of cities and roads.

Space Complexity

The space complexity comes from two main sources: storing the adjacency list and maintaining the visited array. Both require O(n + m) space. Additionally, the DFS recursion stack can go up to O(n) in the worst case for a highly connected component.

Overall, the solution is optimized for large inputs and handles multiple queries efficiently.

Mistakes to Avoid & Tips

Related Problems

If you found Roads and Libraries interesting, you might also like these similar graph problems:

• HackerRank Even Tree
• Connected Cells in a Grid
• BFS: Shortest Reach in a Graph
• Explore more Graph problems on HackerRank

Conclusion

Solving the HackerRank Roads and Libraries problem is an excellent exercise in understanding graph traversal and connected components. By using DFS, we can efficiently determine the optimal placement of libraries and roads to minimize the total cost.

Key takeaways from this problem:

• DFS is an effective way to identify connected components in a graph.
• Always compare the cost of building a library versus repairing a road before making decisions.
• Disconnected cities form separate components and each requires at least one library.
• The solution runs in O(n + m) time and uses O(n + m) space, making it efficient for large inputs.

I encourage you to try more graph problems on HackerRank to strengthen your understanding of DFS, graph traversal, and cost optimization strategies. These skills are highly valuable in competitive programming and technical interviews.