Problem Overview

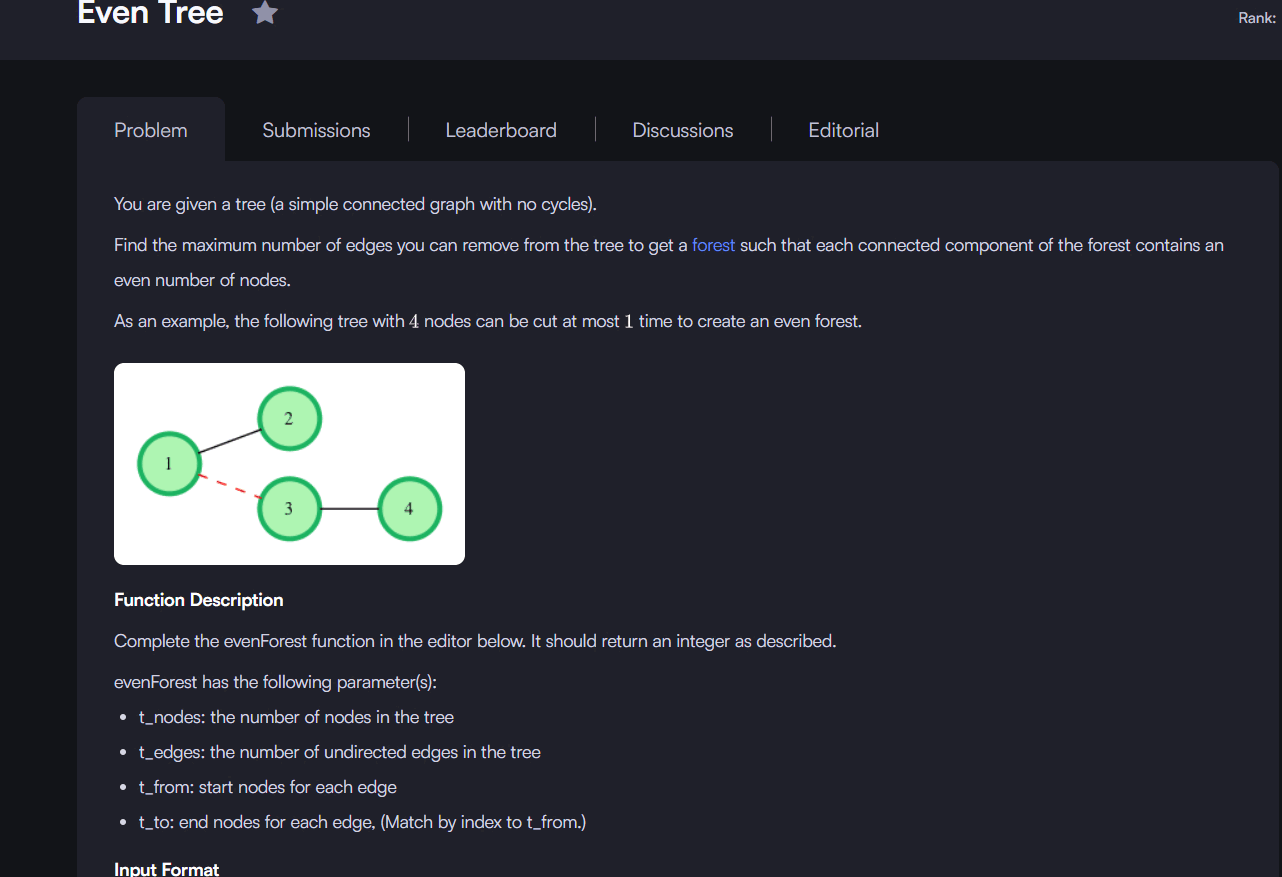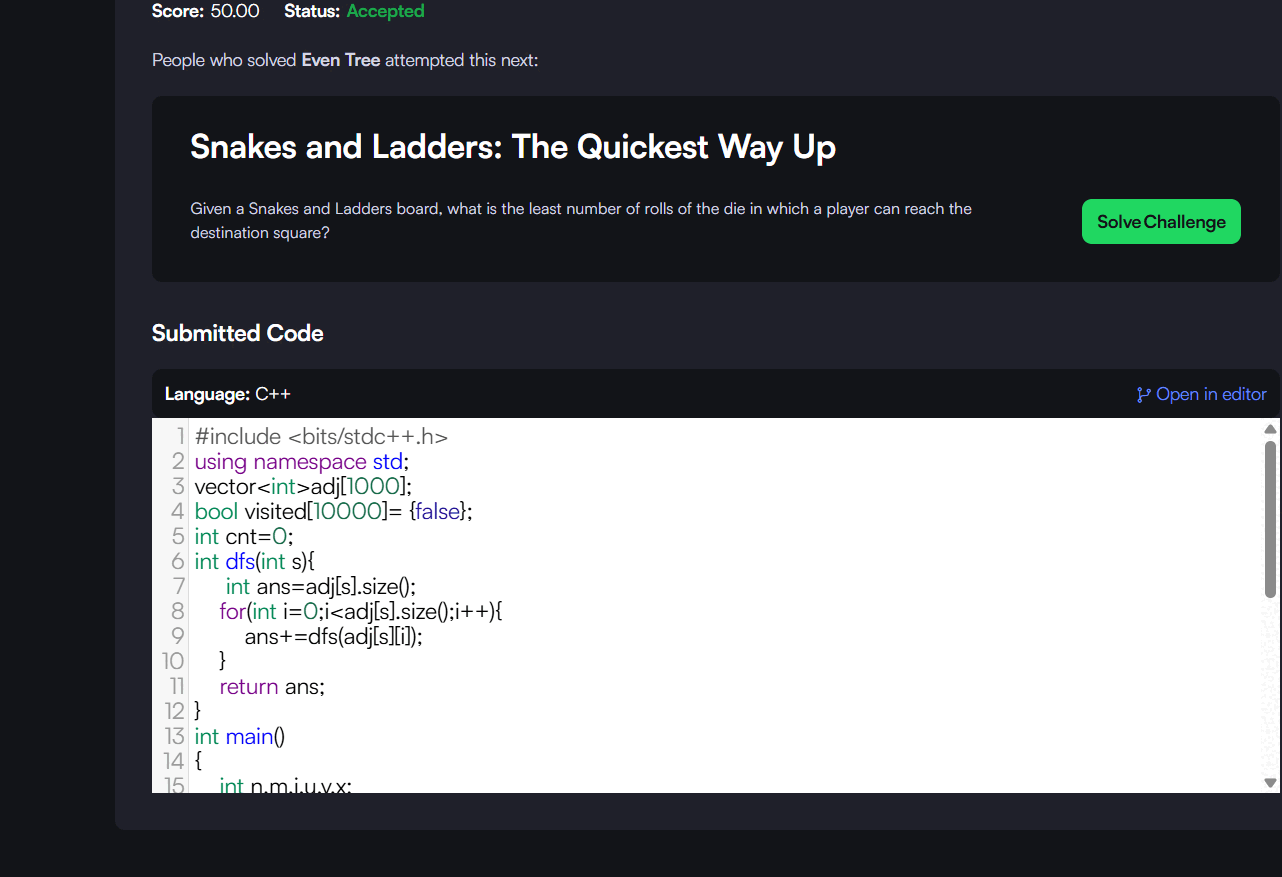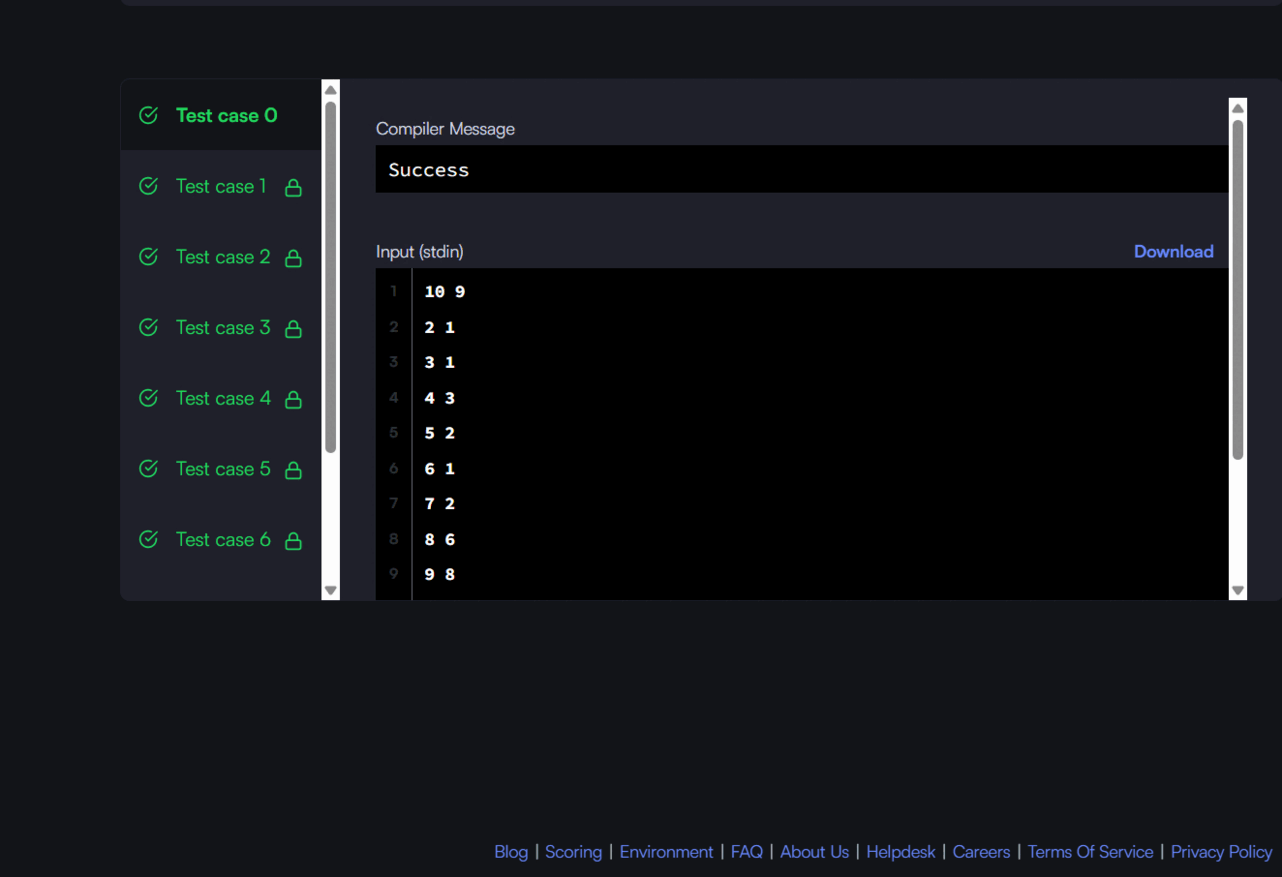
The HackerRank Even Tree problem is a classic graph and tree problem that asks us to maximize the number of edges we can remove from a tree while making sure that every connected component left behind has an even number of nodes. This challenge is interesting because it requires a careful balance of graph traversal and subtree size calculation.

The input provides us with n nodes and m edges of an undirected tree. Since a tree is always connected and has no cycles, the structure is well-defined. Our task is to figure out how many edges can be cut so that all resulting components maintain an even vertex count.

The key observation is that if the size of a subtree (rooted at a given node) is even, then the edge connecting that subtree to its parent can safely be removed. This turns the problem into a subtree size counting problem, which can be solved efficiently with depth-first search (DFS).

This makes the problem not only a good practice for graph traversal techniques but also an important exercise in thinking about tree properties and divide-and-conquer strategies.

Hackerrank Even Tree

Problem Difficulty & Tags

The Even Tree problem on HackerRank is generally classified as a Medium-level problem. It requires understanding of Graph Theory, specifically working with trees, depth-first search (DFS), and recursive subtree calculations.

  • Difficulty: Medium
  • Tags: Graphs, Trees, Depth First Search (DFS), Subtree Sizes

Since the problem revolves around partitioning a tree into components with even nodes, it is an excellent practice for recursion, DFS, and graph traversal logic. It also introduces the idea of solving optimization problems on trees by exploiting structural properties.

Understanding the Problem

The Even Tree problem asks us to work with a tree structure and determine how many edges we can remove such that every resulting subtree has an even number of nodes. The challenge is not just about removing edges randomly, but making sure that each connected component formed after removal still satisfies the condition of having an even number of vertices.

The input provides the number of nodes and edges, followed by pairs representing the edges of the tree. Since it’s a tree, the structure is connected and has exactly n - 1 edges. Our task is to analyze the tree and count the maximum number of edges that can be removed while maintaining the even-node condition.

This problem is a nice application of DFS traversal because we need to calculate the size of each subtree. Once we know the size of a subtree, we can decide whether removing the connecting edge will still keep both components even-sized. If it does, that edge is a valid removal candidate.

Approach / Logic Explanation

To solve this problem, the key idea is to use DFS (Depth First Search) to calculate the size of every subtree. The logic works as follows:

  1. Start from each node and recursively calculate the size of its subtree. The size is simply the total number of nodes in that subtree.
  2. Once we have the subtree size, we check if it is even. If yes, then the edge that connects this subtree to its parent can be safely removed because both resulting parts will still contain even numbers of nodes.
  3. We keep a counter that increments every time we find such a valid removable edge.
  4. Finally, we print the counter which represents the maximum number of edges we can remove.

The beauty of this approach lies in its simplicity: we only need one DFS traversal, and the subtree size information directly tells us whether we can cut the edge or not. Since we are processing each node and edge exactly once, the complexity is O(n), which is efficient enough for the given constraints.

Solution Code

Below is my C++ implementation for the Even Tree problem. It uses DFS to compute subtree sizes and counts the removable edges.

#include <bits/stdc++.h>
using namespace std;

vector<int> adj[1000];
bool visited[10000] = {false};
int cnt = 0;

int dfs(int s) {
    int ans = adj[s].size();
    for (int i = 0; i < adj[s].size(); i++) {
        ans += dfs(adj[s][i]);
    }
    return ans;
}

int main() {
    int n, m, i, u, v, x;
    cin >> n >> m;

    for (i = 0; i < m; i++) {
        cin >> u >> v;
        adj[v].push_back(u);
    }

    for (i = 2; i <= n; i++) {
        x = dfs(i);
        if (x % 2 == 1)
            cnt++;
    }

    cout << cnt << endl;
    return 0;
}

Step-by-Step Walkthrough

Let me explain how my DFS-based solution works using a small example tree:

Example:

Number of nodes (n) = 10
Edges:

2 → 1
3 → 1
4 → 3
5 → 2
6 → 1
7 → 2
8 → 6
9 → 8
10 → 8
Graph diagram

 

  1. DFS Traversal: I start DFS from each node to calculate the size of its subtree.
  2. Compute Subtree Size: For example, the subtree rooted at node 8 has nodes 8, 9, 10 → size = 3.
  3. Check for Edge Removal: Since the size is odd, I don’t remove the edge 8→6. For subtrees with even size, the connecting edge can be removed.
  4. Update Counter: Each time a removable edge is found, increment cnt.
  5. Final Answer: After DFS for all nodes, cnt contains the maximum number of removable edges that satisfy the even-node condition.

This walkthrough shows how the DFS efficiently computes subtree sizes and determines removable edges, making the solution both correct and optimal.

Sample Input & Output

To help visualize the solution, here’s an example of input and the corresponding output:

Input Output Explanation
10 9
2 1
3 1
4 3
5 2
6 1
7 2
8 6
9 8
10 8		 2 The tree can have 2 edges removed so that all resulting components contain an even number of nodes.

Time & Space Complexity Analysis

Time Complexity

The DFS traversal visits each node and edge exactly once. Since a tree has n nodes and n-1 edges, the overall time complexity is O(n). This ensures the solution runs efficiently even for large trees.

Space Complexity

The space complexity comes from storing the adjacency list and the recursion stack. The adjacency list requires O(n) space, and the DFS recursion stack may go up to O(n) in the worst case. So the total space complexity is O(n).

Overall, this approach is efficient and suitable for the constraints typically given in HackerRank tree problems.

Mistakes to Avoid & Tips

Warning: Don’t forget that removing an edge with an odd-sized subtree will break the even-node condition. Always check subtree size before removing.
Common Error: Trying to remove edges without calculating subtree sizes can lead to incorrect results. DFS is essential to get accurate counts.
Pro Tip: Start DFS from the leaves and move up. This way, you can calculate subtree sizes efficiently and decide removable edges in a single pass.
Note: Remember that trees with all odd-sized subtrees may not allow any edges to be removed. Always handle these edge cases in your logic.

Related Problems

If you found this problem interesting, you might also like these similar challenges:

Conclusion

Solving the HackerRank Even Tree problem is a great exercise for understanding tree traversal and subtree properties. Using DFS to calculate subtree sizes allows us to efficiently determine which edges can be removed while keeping all resulting components even-sized.

Key takeaways from this problem:

  • DFS is ideal for computing subtree sizes in a tree.
  • Only edges connected to even-sized subtrees can be safely removed.
  • The solution runs in O(n) time and uses O(n) space, making it efficient for large inputs.

I encourage you to try more graph and tree problems on HackerRank to strengthen your understanding of recursion, graph traversal, and tree optimization techniques. These concepts are widely used in coding interviews and competitive programming challenges.